Logarithm And Natural Log Rules
May 7 2015 nbsp 0183 32 You ll need to complete a few actions and gain 15 reputation points before being able to upvote Upvoting indicates when questions and answers are useful What s reputation and how do I get it Instead you can save this post to reference later The logarithm does not. And if the power of the numerator is greater, the rational function grows at least linearly; the logarithm does not. So there is no rational function (or polynomial) that can approximate the logarithm for large values. That being said, rational functions called Pade approximations beat truncated power series.

Mar 22 2013 nbsp 0183 32 natural logarithm natural log en wikipedia wiki T Pronouncing ln x el en Logarithms are defined as the solutions to exponential equations and so are practically useful in any situation where one needs to solve such equations (such as finding how long it will take for a population to double or for a bank balance to reach a given value with compound interest). Historically, they were also useful because of the fact that the logarithm of a product is the sum …
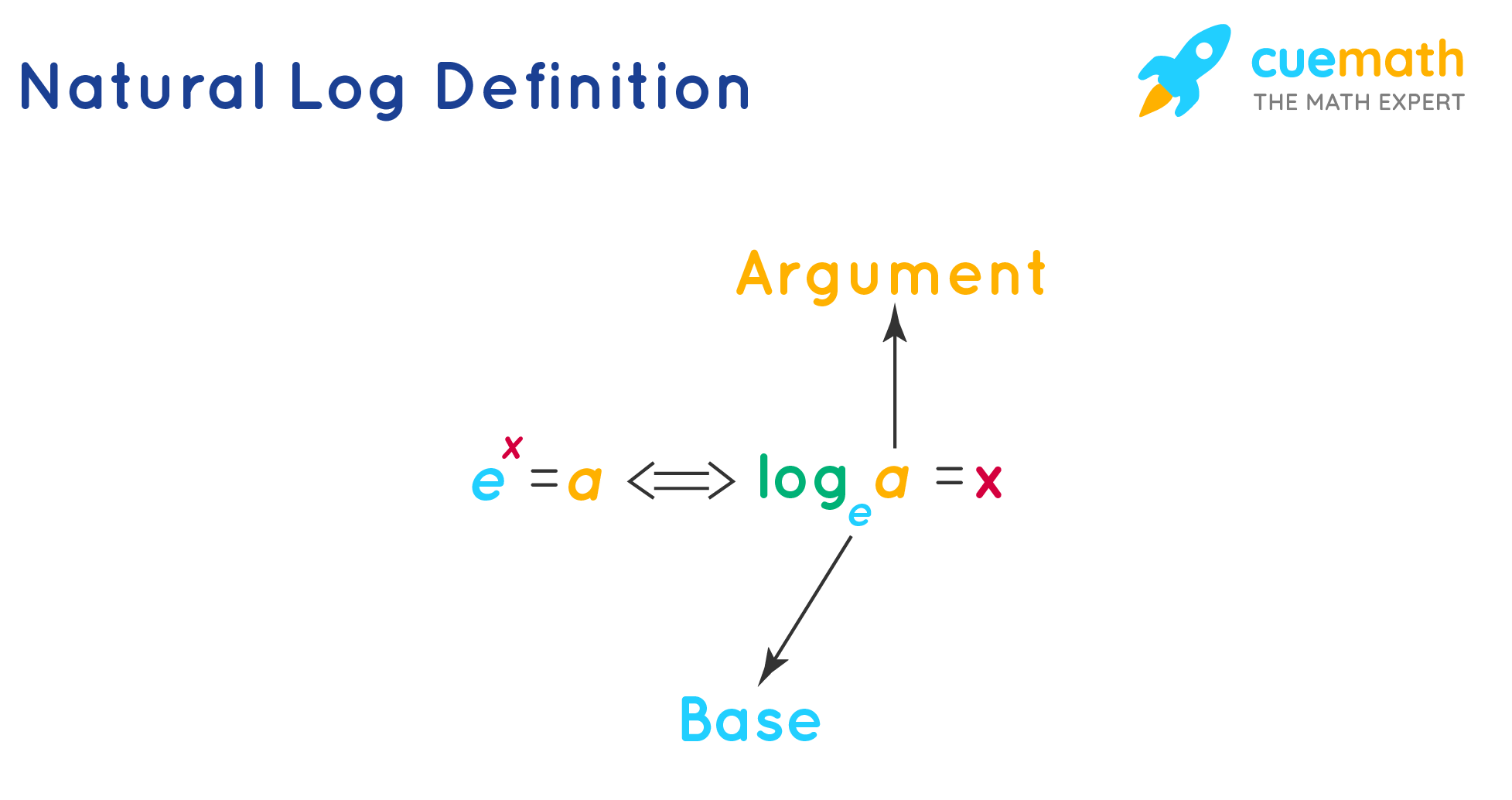
Logarithm And Natural Log Rules
Log logarithm ln natural logarithm lg Core pure 3 notes integrals involving the natural logarithm function. Derivative of log calculator passachildUnit 3 exponents logarithms worksheets library.

Logarithms The Easy Way Worksheets Library
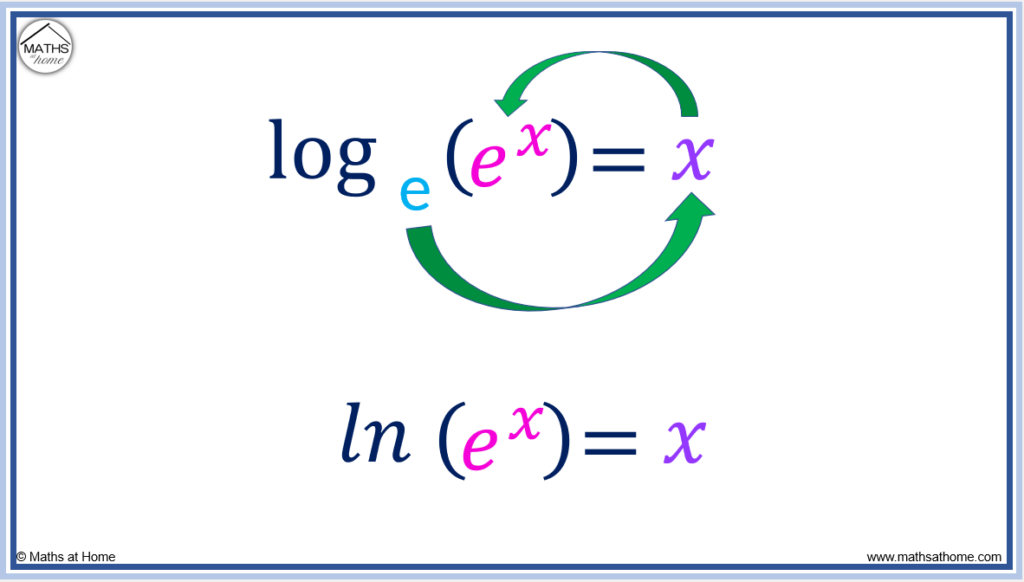
How To Write In Logarithmic Form Mathsathome
Oct 25 2024 nbsp 0183 32 Since the real logarithm is continuous Log Log is continuous Arg Arg is continuous However I have no idea how to prove rigorously that Arg Arg is continuous Do you have any suggestion Thanks for any help You are seriously doing this for fun? I know that my parents had to use logarithm tables when there were no affordable calculators. Why would you want to do this by hand today?
Nov 29 2013 nbsp 0183 32 Does anyone know a closed form expression for the Taylor series of the function f x log x where log x denotes the natural logarithm function Jan 9, 2017 · This is called the principal complex logarithm and is usually denoted by $\operatorname {Log}$ (capital L). Technically, it doesn't matter to what range you restrict $\theta$, as long as the resulting logarithm is a proper function (not a multivalued function) and you are consistent in your restriction of $\theta$.