Multiplication Tables Worksheet Pdf
Oct 14 2016 nbsp 0183 32 For ndarrays is elementwise multiplication Hadamard product while for numpy matrix objects it is wrapper for np dot As the accepted answer mentions np multiply always returns an elementwise multiplication Dec 23, 2012 · To multiply, just do as normal fixed-point multiplication. The normal Q2.14 format will store value x/2 14 for the bit pattern of x, therefore if we have A and B then So you just need to multiply A and B directly then divide the product by 2 14 to get the result back into the form x/2 14 like this AxB = ((int32_t)A*B) >> 14;

Dec 6 2013 nbsp 0183 32 How would I make a multiplication table that s organized into a neat table My current code is n int input Please enter a positive integer between 1 and 15 for row in range 1 n 1 for Following normal matrix multiplication rules, an (n x 1) vector is expected, but I simply cannot find any information about how this is done in Python's Numpy module.
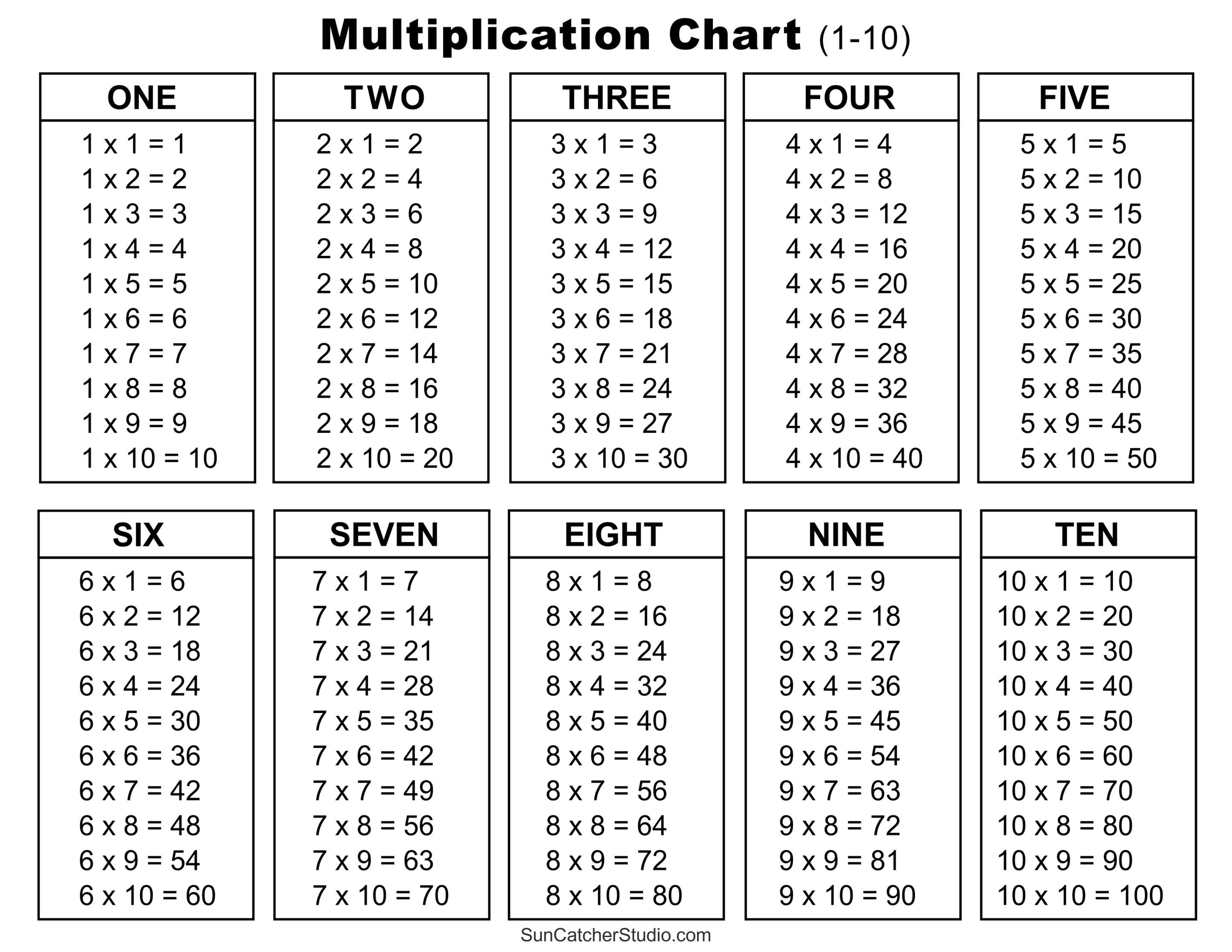
Multiplication Tables Worksheet Pdf
Jul 26 2022 nbsp 0183 32 How can I perform multiplication using bitwise operators Asked 14 years 11 months ago Modified 1 year 7 months ago Viewed 121k times Printable times tables worksheets activity shelter. 12 times table worksheet 12 multiplication table free pdfTables 12 to 20 multiplication tables 12 to 20 onlymyenglish.

Multiplication
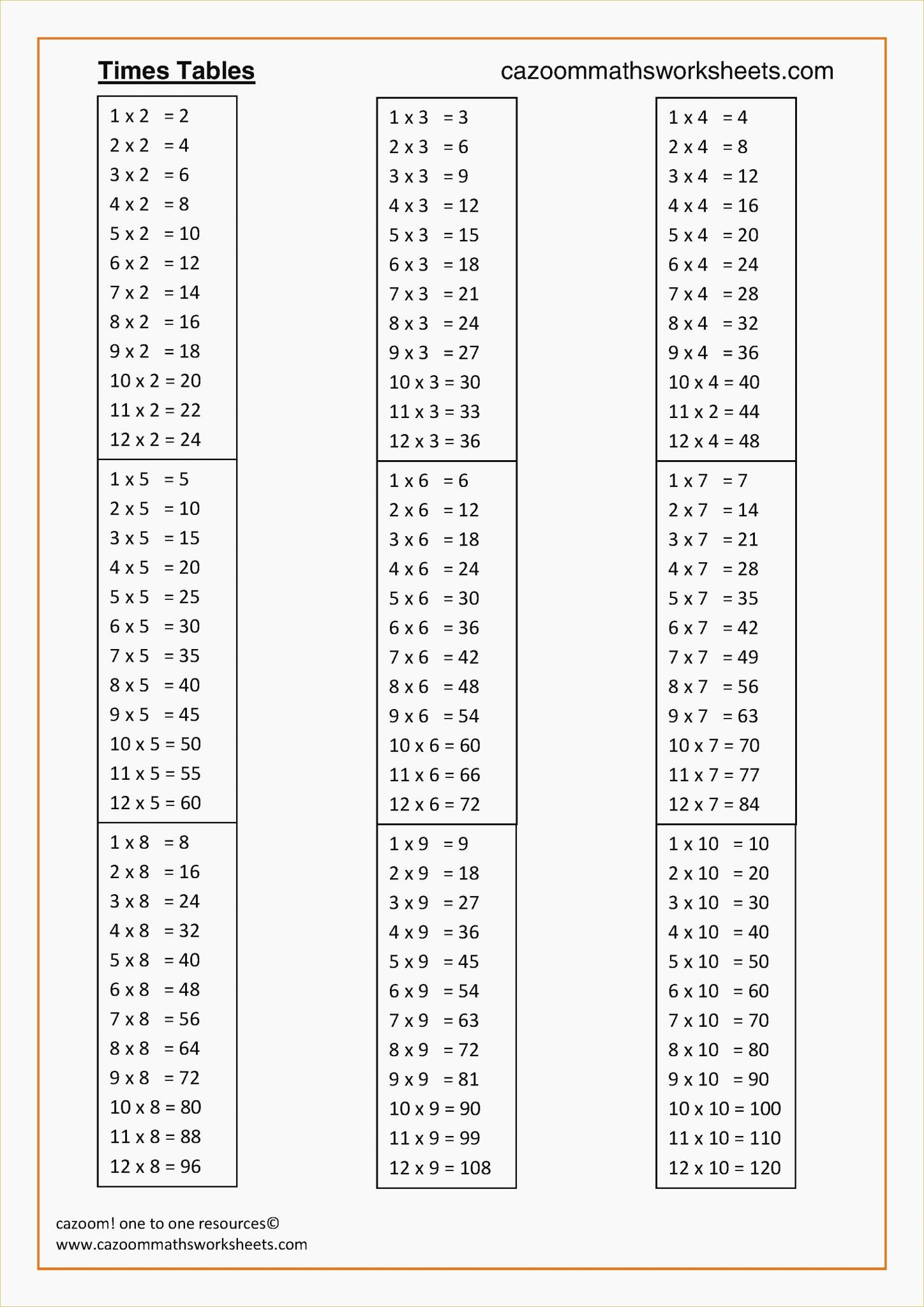
Multiplication Quiz Printable
Dec 15 2009 nbsp 0183 32 Since multiplication is more expensive than addition you want to let the machine paralleliz it as much as possible so saving your stalls for the addition means you spend less time waiting in the addition loop than you would in the multiplication loop This is just my logic Others with more knowledge in the area may disagree I need frequent usage of matrix_vector_mult() which multiplies matrix with vector, and below is its implementation. Question: Is there a simple way to make it significantly, at least twice, faster?
Jan 22 2017 nbsp 0183 32 The fastest known matrix multiplication algorithm is Coppersmith Winograd algorithm with a complexity of O n 2 3737 Unless the matrix is huge these algorithms do not result in a vast difference in computation time In practice it is easier and faster to use parallel algorithms for matrix multiplication Does Verilog take care of input and output dimensions when multiplying signed numbers? To be specific, what happens if I multiply a signed 32-bit with a signed 64-bit number? If I have: reg signed...